析合树学习笔记

学习析合树：
step1 ：爆%机房巨佬Laffey
step剩下的：听Laffey讲课
~~学习笔记结束~~

参考内容：巨佬Laffey的讲课内容、Laffey的博客、oi_wiki
引入问题： CF526F

给定一个$n \times n$的棋盘，其中有$n$个棋子，每行每列恰有一个。
求有多少个$k \times k$的棋盘中恰好有$k$个棋子。($n \le 3 \times 10^5$)

我们首先把问题抽象化：已知每行每列恰有一个棋子，那么我们可以把原棋盘抽象成一个存储棋子纵坐标的数列，那么原问题转化为求该数列中值域连续的区间个数。
例如原棋盘为：

$\begin{bmatrix} \bigcirc & & & \\ & & \bigcirc & \\ & \bigcirc & & \\ & & & \bigcirc \end{bmatrix}$

我们就可以把它抽象为数列：

$4,2,3,1$

我们发现既然每行有且只有一个棋子，那么最终的数列应当是1~n的一个排列

那么要求解的也就是这个数列中数值连续（指值域没有断点）的区间个数

其中，我们把每个值域连续的区间称为一个连续段，然而一个排列

我们引入本原连续段的概念：

对于一个排列P，我们认为一个本原连续段M表示在集合$I_p$ 中，不存在与之相交且不包含的连续段

所以由定义显然，本源段之间只能包含/相离，多个（包含2）相邻的本源段可以构成连续段

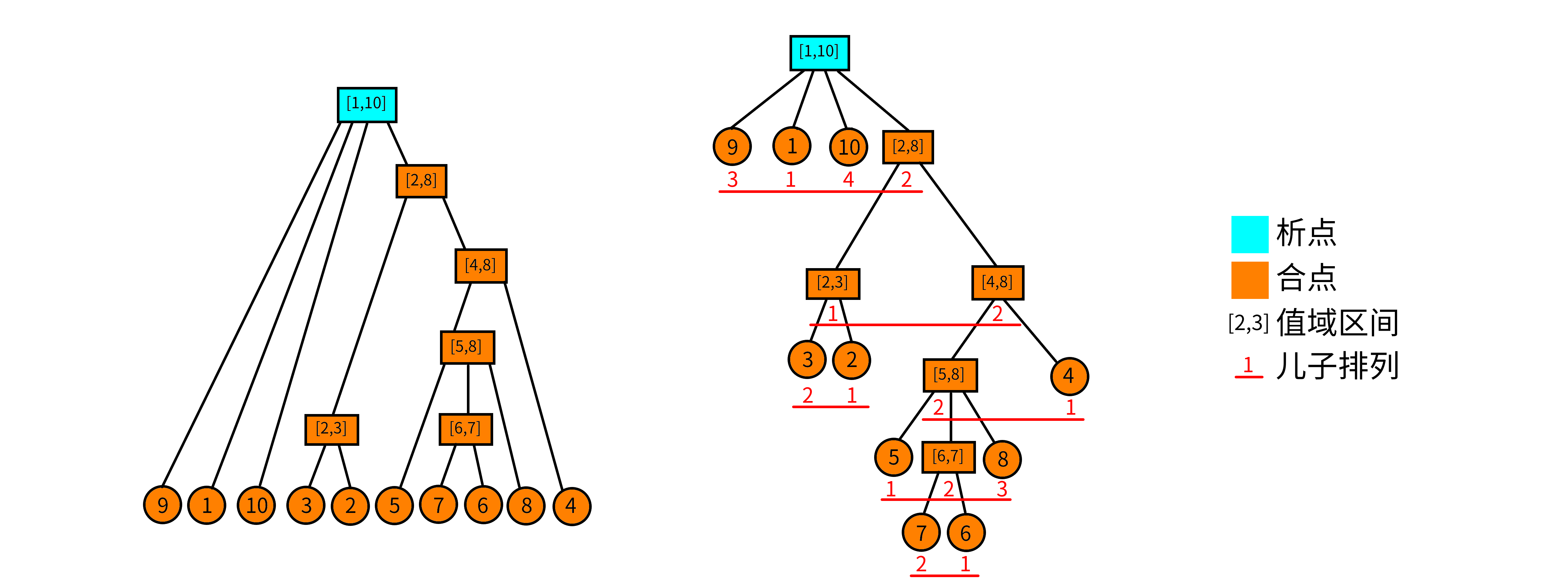
所以对于一个排列$P=\{9,1,10,3,2,5,7,6,8,4\}$，其本源连续段可以构成这样一棵析合树：

（图片来源于oi-wiki）

图中蓝点为析点，橙点为合点。图中每个节点都是一个本源段，表明了其值域

那么下面引入一些析合树的基本概念：

儿子序列：将当前区间的所有子区间按照值域排列的有序序列称为儿子序列，无关其在原数列中的位置，比如节点 [4,8][4,8] 的儿子序列为 $\lbrace 4 \rbrace \lbrace [5,8] \rbrace{4}{[5,8]}$，而非原数列中的顺序 $\lbrace [5,8] \rbrace \lbrace 4 \rbrace{[5,8]}{4}$ 。

儿子排列：将一个节点的儿子序列离散化成正整数后形成的排列为儿子排列。即儿子序列中元素的排名按照原数列的顺序所形成的排列，比如图中 [1,10][1,10] 的儿子排列为 $\{3,1,4,2 \}$ 。

合点：儿子排列单调上升或单调下降的节点为合点。（其儿子序列的值域首尾相接）

析点：不是合点的节点均为析点。

叶子节点是析点还是合点的问题说法不一，我们姑且认为叶子节点为合点。
（定义CV自Laffey的博客）

由定义我们可以得到一个合点的重要性质： 有序性。例如上图代表区间$[1,10]$的点为析点，因为其内部儿子序列不满足有序性。

合点还具有另外一个性质：对于一个合点，其儿子序列的任意子区间都构成一个连续段

析点的性质是：对于一个析点，其儿子序列的任意元素个数大于1的子区间都不构成一个连续段

因为我没看看不懂构建析合树的线性算法，所以我就简单说一下简单一点的$O(n\space log \space n)$算法： 增量法

用一个栈来存储当前的析合森林（栈中节点是某棵小析合树的根，为析点或合点），最终显然栈中只会剩下一棵析合树——构建完成的析合树

那么我们考虑向栈中添加节点的过程，此时如何将新节点与旧节点合并：

判断当前节点能否成为栈顶结点的儿子，若能，就把他加入栈顶结点的儿子序列，取出栈顶作为当前节点继续，若不能则往下看：
判断当前节点能否与几个栈顶结点合并成一个合点，若能，则合并，将合并后节点作为当前节点
判断当前节点能否和几个栈顶结点合并成为一个析点，若能，则合并，将合并后节点作为当前节点
重复上述过程至不能再重复为止，然后把当前节点压栈。

所以我们发现上述操作的难点在于判断能否合并的过程：我们不能接受暴力判能否合并的时间复杂度

Laffey：“所以我们需要考虑使用值域连续段的判定方式进行优化。首先判断两个区间是否值域连续很简单，可以使用 $ST$ 表维护区间最值。”

所以对于操作1，当前节点只能成为合点的儿子（因为成为析点儿子后析点将存在一子连续段——能合并则必然有一相邻连续段，则不满足析点性质）

对于操作2、3，则是复杂度瓶颈，那么我们考虑枚举栈顶的边界：即求出每个单点$i$所能合并区间的最左端$L_i$ ：
显然对于一个连续段l~r，我们有：

$\max_{l \le i \le r}P_i - \min_{l \le i \le r} = r - l$

（读者自证不难）
所以对于任意段都有:

$Q_j = \max_{j \le k \le i}P_k - \min_{j \le k \le i} - i + j \ge 0$

显然，我们只要维护满足这个式子的最小值为0的最小j即为所求$L_i$于是看到区间最小值，我们考虑线段树，可以维护

那么考虑变化：当当前增量结束，i变为i+1时上式的值显然可能变化。如何变化？

如果 $P_{i+1}>max$ ，相当于我们把 $Q_j$ 先减掉 $max$ 再加上 $P_{i+1}$ 就完成了 $Q_j$ 的更新；$P_{i+1} < mix$ 同理，相当于 $Q_j = Q_j+min-P_{i+1}$ .

那么如果对于一个区间 $[x,y]$，满足 $P_{x~i},P_{x+1~i}, \cdots ,P_{y~i}$ 的区间 $max$ 都相同呢？你已经发现了，那么相当于我们在做一个区间加的操作；同理，当 $[x,y]$，满足 $P_{x~i},P_{x+1~i}, \cdots ,P_{y~i}$ 的区间 $min$ 都相同时也是一个区间加的操作。同时，$max$ 和 $min$ 的更新是相互独立的，因此可以各自更新。

因此我们对 $Q$ 的维护可以这样描述：

找到最大的 $j$ 使得 $P_j > p_{i+1} $，那么显然，这一段数全部小于 $P_{i+1}$ ，于是就需要更新 $Q_{j+1~i} $ 的最大值。由于 $P_i,max(P_i,p_{i-1}),\cdots ,max(P_i,p_{i+1},\cdots,P_{j+1})$ 是（非严格）单调递增的，因此可以每一段相同的做相同的更新，即区间加操作。

更新 $min$ 同理。

把每一个 $Q_j$ 都减 $1$ 。因为区间长度加 $1$。

查询：即查询 $Q$ 的最小值的所在的下标。

那么现在的问题时如何找到相同的一段使得他们的极值相同，~~显然这是一道单调栈板子题~~所以肯定用单调栈来维护，于是在更新单调栈（弹栈）的时候顺便更新线段树即可

最后放一张oi—wiki上的图来辅助理解：

图片来源于oi-wiki